Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 운영체제
- 99일지
- 국비
- AWS
- 99클럽
- 자바
- 내일배움캠프
- 부트캠프
- Flutter
- 개발자블로그
- 스파르타코딩클럽
- 컴퓨터개론
- 스파르타내일배움캠프
- 개발자스터디
- 중심사회
- Python
- 백준
- 항해
- 프로그래머스
- Spring
- til
- 스파르타내일배움캠프TIL
- MySQL
- 소프트웨어
- 코딩테스트
- 스파르타내일배움캠프WIL
- 컴퓨터구조론 5판
- wil
- java
- 개인공부
Archives
- Today
- Total
컴공생의 발자취
[Algorithm] 선택 문제 Selection Problem - C언어 본문
728x90
반응형
분할 정복 알고리즘(Divide-and-Conquer)
선택 문제(Selection Problem)
: k번째 작은 수를 찾는 문제
입력에서 퀵 정렬에서와 같이 피봇을 선택하여 피봇보다 작은 부분과 큰 부분으로 분할한 후에 k번째 작은 수가 들어 있는 부분을 순환적으로 탐색한다.
unsorted array : 최소 숫자를 k번 찾는다.
-> 최악 시간복잡도 : O(kn)
** 단, 최소 숫자를 찾은 뒤에는 입력에서 최소 숫자를 제거한다.
sorted array : 숫자들을 정렬한 후, k번째 숫자를 찾는다.
-> 최악 시간복잡도 : O(nlogn)
pseudo code
Selection(A, left, right, k)
입력 : A[left] ~ A[right]와 k. 단, 1<=k<=|A|, |A|=right-left+1
출력 : A[left] ~ A[right]에서 k번째 작은 원소
피봇을 A[left] ~ A[right]에서 랜덤하게 선택하고, 피봇과 A[left]의 자리를 바꾼 후,
피봇과 배열의 각 원소를 비교하여 피봇보다 작은 숫자는 A[left] ~ A[p-1]로 옮기고,
피봇보다 큰 숫자는 A[p+1] ~ A[right]로 옮기며, 피봇은 A[p]에 놓는다.
S = (p-1)-left+1 // S = Small group의 크기
if(k <= S) Selection(A, left, p-1, k) // Small group에서 찾기
else if (k = S+1) return A[p] // 피봇 = k번째 작은 숫자
else Selection(A, p+1, right, k-S-1) // large group에서 찾기
시간복잡도
- 평균 시간복잡도 : O(n)
-> O[n + 3/4n + (3/4)^2 * n + ... + (3/4)^(i-1) * n + (3/4)^i * n] = O(n)
-> 평균 2번만에 good 분할이 되므로 2 X O(n) = O(n)
구현 - C언어
#include <stdio.h>
#define MAX_SIZE 12
int SelectionProb(int arr[], int left, int right, int find_idx);
int Pivot(int arr[], int left, int right);
void Swap(int arr[], int x, int y); // 값 교환
void PrintArr(int arr[]); // 배열 출력
int main(void) {
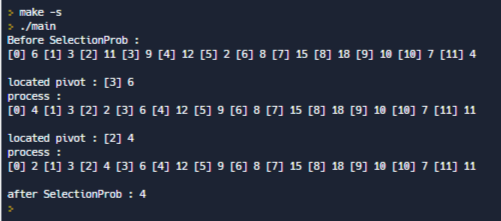
int arr[MAX_SIZE] = {6, 3, 11, 9, 12, 2, 8, 15, 18, 10, 7, 4};
int result = 0;
// SelectionProb 수행 전 배열 출력
printf("Before SelectionProb : \n");
PrintArr(arr);
// SelectionProb 수행
// (배열, left: 배열의 시작, right: 배열의 끝, find_idx: k번째 작은 수)
result = SelectionProb(arr, 0, MAX_SIZE - 1, 3);
// 결과 출력
printf("after SelectionProb : %d\n", result);
return 0;
}
int SelectionProb(int arr[], int left, int right, int find_idx) {
// pivot을 기준으로 분할 후 정렬
int p_idx = Pivot(arr, left, right);
// QuickSort 과정 출력
printf("located pivot : [%d] %d \n", p_idx, arr[p_idx]);
printf("process : \n");
PrintArr(arr);
// k번째 작은 수를 찾은 경우
if (p_idx == find_idx - 1)
return arr[p_idx];
// k번째 작은 수가 왼쪽 배열(pivot기준 작은 값)에 속한 경우
else if (p_idx > find_idx - 1)
// left ~ pivot-1 인덱스 부분의 배열 정렬
return SelectionProb(arr, left, p_idx - 1, find_idx);
// k번째 작은 수가 오른쪽 배열(pivot 기준 큰 값)에 속한 경우
else
// pivot+1 ~ right 인덱스 부분의 배열 정렬
return SelectionProb(arr, p_idx + 1, right, find_idx);
}
int Pivot(int arr[], int left, int right) {
int low = left;
int hight = right;
// 정렬할 배열의 가장 왼쪽 데이터를 pivot로 선택
int pivot = arr[left];
while (low < hight) {
// arr[low]의 값이 pivot보다 작으면 계속 증가
while (low <= right && arr[low] < pivot) {
low++;
}
// arr[hight]의 값이 pivot보다 크면 계속 증가
while (hight >= left && arr[hight] > pivot) {
hight--;
}
// 앞서 while에서 pivot과 비교하였을 때
// arr[low]>pivot && arr[hight]<pivot일 경우
if (low < hight) {
// arr[low]와 arr[hight]의 값 교환
Swap(arr, low, hight);
}
}
// arr의 인덱스인 low와 hight의 값이 같아지면
// pivot(arr[left])과
// arr[hight](pivot이 있어야 위치)의 값을 교환
Swap(arr, low, hight);
// pivot의 위치
return hight;
}
void Swap(int arr[], int x, int y) {
int tmp;
tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
void PrintArr(int arr[]) {
for (int i = 0; i < MAX_SIZE; i++) {
printf("[%d] %d ", i, arr[i]);
}
printf("\n\n");
}
결과
728x90
반응형
'📖 이론 > 컴퓨터 알고리즘' 카테고리의 다른 글
| [Algorithm] 퀵 정렬 QuickSort - C언어 (0) | 2023.04.28 |
|---|---|
| [Algorithm] 합병정렬 MergeSort - C언어 (0) | 2023.04.24 |


