3.1 부호화 크기는 맨 좌측 비트가 부호비트이고, 나머지 비트들은 수의 크기를 나타낸다. 어떤 양수에 대하여 1의 보수와 2의 보수로 표현한 결과는 동일하다.
(1) 8-비트 길이의 부호화-크기 : 0001 0011
1의 보수 : 0001 0011
2의 보수 : 0001 0011
(2) 8-비트 길이의 부호화-크기 : 1001 0011
1의 보수 : 1110 1100
2의 보수 : 1110 1101
(3) 8-비트 길이의 부호화-크기 : 0111 1100
1의 보수 : 0111 1100
2의 보수 : 0111 1100
(4) 8-비트 길이의 부호화-크기 : 1111 1100
1의 보수 : 1000 0011
2의 보수 : 1000 0100
3.2 부호-비트를 확장하는 경우 부호화-크기 표현에서는 부호 비트를 새로운 맨 좌측 위치로 이동시키고, 그 외의 위치들은 0으로 채우면 된다. 보수는 양수인 경우 모든 상위 비트들을 0으로 세트하고, 음수의 경우에는 1로 세트한다.
(1) 16-비트 길이의 부호화-크기 : 0000 0000 0001 0011
1의 보수 : 0000 0000 0001 0011
2의 보수 : 0000 0000 0001 0011
(2) 16-비트 길이의 부호화-크기 : 1000 0000 0001 0011
1의 보수 : 1111 1111 1110 1100
2의 보수 : 1111 1111 1110 1101
(3) 16-비트 길이의 부호화-크기 : 0000 0000 0111 1100
1의 보수 : 0000 0000 0111 1100
2의 보수 : 0000 0000 0111 1100
(4) 16-비트 길이의 부호화-크기 : 1000 0000 0111 1100
1의 보수 : 1111 1111 1000 0011
2의 보수 : 1111 1111 1000 0100
3.3 10진수로 변환 -128 + (1 + 2^2 + 2^3 + 2^5 + 2^6)
= -128 + (1 + 4 + 8 + 32 + 64)
= -19
양수로 바꾸고 10진수로 변환 1110 1101 → 0001 0011
-(1 + 21 + 24)
= -(1 + 2 + 16)
= -19
따라서, 두 결과 값이 일치한다.
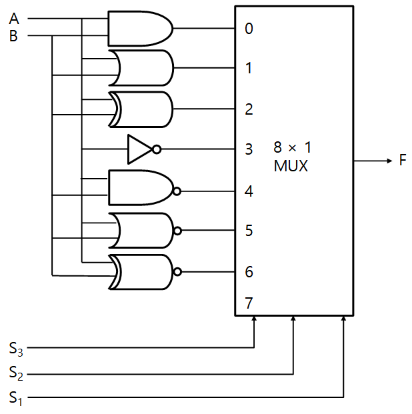
3.4

3.5
(1) 1000 0001
(2) 1110 1111
(3) 0110 1110
3.6

3.7 1110 0000을 마스크 연산(AND 연산)를 사용하여 A레지스터의 값을 1101 0010에서 1100 0000으로 저장한 후, 0000 1110을 선택적-세트(OR 연산)를 사용하여 A레지스터의 값을 1100 0000에서 1100 1110으로 저장한다.
3.8
(1) 0110 1001
(2) 1010 0100
(3) 0110 1001
(4) 1010 0101
(5) 1110 1001
(6) 1010 0100
3.9
(1) 0101 1001
(2) 1011 0010
(3) 1101 1001
(4) 1011 0010
3.10
(1) 0101 1001, C 플래그 : 0
(2) SHLC 첫 번째 : 1011 0010, C 플래그 : 0 SHLC 두 번째 : 0110 0100, C 플래그 : 1
3.11 초기 상태에서 어떤 레지스터에 ‘1011 0011’이 저장되어 있고, C 플래그의 값은 ‘1’이라고 하자.
(1) 0110 0111, C 플래그 : 1
(2) RRC 첫 번째 : 1011 0011, C 플래그 : 1
RRC 두 번째 : 1101 1001, C 플래그 : 1
3.12 오버플로우(V)는 최상위 비트의 캐리(올림수)와 그 다음 비트들의 덧셈 과정에서 발생하는 캐리가 서로 다른 경우에 발생한다. 즉 V = C최상위 비트 ⊕ C그 다음 비트
(1) 100100 + 111010 = 011110이고 C6 = 1(최상위 비트의 캐리), C5 = 0(최상위 비트 다음비트의 캐리)이므로 오버플로우가 발생한다.
(2) 1100 1100 + 1011 1010 = 1000 0110이고 C8 = 1(최상위 비트의 캐리), C7 = 1(최상위 비트 다음비트의 캐리)이므로 오버플로우가 발생하지 않는다.
3.13
56 : 0011 1000
-56 : 1100 1000
89 : 0101 1001
-89 : 1010 0111
(1) 89 – 56 = 89 + (-56) = 0101 1001 + 1100 1000 = 0010 0001
C8 = 1, C7 = 1이므로 오버플로우가 발생하지 않는다.
(2) (-56) – 89 = (-56) + (-89) = 1100 1000 + 1010 0111 = 0010 1111
C8 = 1, C7 = 0이므로 오버플로우가 발생한다.
(3) 56 – (-89) = 56 + 89 = 0011 1000 + 0101 1001 = 1001 0001
C8 = 0, C7 = 1이므로 오버플로우가 발생한다.
(4) 56 – 89 = 56 + (-89) = 0011 1000 + 1010 0111 = 1101 1111
C8 = 0, C7 = 0이므로 오버플로우가 발생하지 않는다.
3.14
| 연산 내용 | 연산 결과 | C | S | Z | V |
| R1 + 1100 0110 | 0011 1000 | 1 | 0 | 0 | 0 |
| R1 + 0001 1110 | 1001 0000 | 0 | 1 | 0 | 1 |
| R1 AND 1000 1101 | 0000 0000 | 0 | 0 | 1 | 0 |
| R1 ⊕ R1 | 0000 0000 | 0 | 0 | 1 | 0 |
3.15
| C | A | Q | M | 연산 내용 | |
| [초기 상태] | 0 | 0000 | 0111 | 1001 | |
| [주기 1] | 0 | 1001 | 0111 | 1001 | Q0=1이므로, A←A+M |
| 0 | 0100 | 1011 | 1001 | 우측 시프트 (C – A –Q) | |
| [주기 2] | 0 | 1101 | 1011 | 1001 | Q0=1이므로, A←A+M |
| 0 | 0110 | 1101 | 1001 | 우측 시프트 (C – A –Q) | |
| [주기 3] | 0 | 1111 | 1101 | 1001 | Q0=1이므로, A←A+M |
| 0 | 0111 | 1110 | 1001 | 우측 시프트 (C – A –Q) | |
| [주기 4] | 0 | 0011 | 1111 | 1001 | Q0=0이므로, 우측 시프트 (C – A –Q) |
3.16
| A | Q | Q-1 | 계수 | M | 연산 내용 | |
| [초기 상태] | 00000 | 01101 | 0 | 5 | 10101 | |
| [주기 1] | 01011 | 01101 | 0 | 10101 | Q0 = 1, Q-1 = 0이므로 A ← A - M | |
| 00101 | 10110 | 1 | 4 | 10101 | 산술적 우측 시프트 | |
| [주기 2] | 11010 | 10110 | 1 | 10101 | Q0 = 0, Q-1 = 1이므로 A ← A + M | |
| 11101 | 01011 | 0 | 3 | 10101 | 산술적 우측 시프트 | |
| [주기 3] | 01000 | 01011 | 0 | 10101 | Q0 = 1, Q-1 = 0이므로 A ← A - M | |
| 00100 | 00101 | 1 | 2 | 10101 | 산술적 우측 시프트 | |
| [주기 4] | 00010 | 00010 | 1 | 1 | 10101 | Q0 = 1, Q-1 = 1이므로 산술적 우측 시프트 |
| [주기 5] | 10111 | 00010 | 1 | 10101 | Q0 = 0, Q-1 = 1이므로 A ← A + M | |
| 11011 | 10001 | 0 | 0 | 10101 | 산술적 우측 시프트 |
3.17

3.18 바이어스가 127이므로 (지수 필드 – 0111 1111)의 값을 십진수하면 된다.
(1) 1111 1110 – 0111 1111 = 0111 1111 = 127
(2) 0111 1111 – 0111 1111 = 0000 0000 = 0
(3) 1011 0101 – 0111 1111 = 0011 0110 = 54
(4) 0010 1101 – 0111 1111 = 0010 1101 + 1000 0001 = 1010 1110 = -(0101 0010) = -82
3.19
(1) 소수점을 구하는 방법은 소수 부분을 0이 될 때까지 2를 계속 곱하고 곱할 때 마다 정수부분이 2진수가 된다.
0.625 × 2 = 1.250
0.250 × 2 = 0
.50.5 × 2 = 1
따라서, 0.625(10) = 0.101(2)
-1.625(10) = -1.101(2) = (-1) × 2^1 × 0.1101
바이어스가 128인 32-비트 부동소수점 형식 : 1 10000001 10100000000000000000000
(2) 바이어스가 256인 64-비트 부동소수점 형식 :
1 100000001 101000000000000000000000000000000000000000000000000000
3.20
(1) 510 = 1012 = 1.012 × 22
0 10000001 01000000000000000000000
(2) 253.2510 = 11111101.012 = 1.1111101012 × 2
70 10000110 11111010100000000000000
(3) -1.62510 = -1.1012 = (-1) × 1.101
21 01111111 10100000000000000000000
(4) -1 / 32 = (-1) × 2-5
1 01111010 00000000000000000000000
3.21
(1) S = 0, E = 131, M = 101(2)
(-1)^0 × 2^(131 – 127) × (1.101(2)) = (-1)^0 × 2^(131 – 127) × (1.625(10)) = 26
(2) S = 1, E = 124, M = 01101(2)
(-1)^1 × 2^(124 – 127) × (1.01101(2)) = (-1)^1 × 2^(124 – 127) × (1.40625(10)) = -0.17578125
(3) S = 1, E = 213, M = 110101(2)
(-1)^1 × 2^(213 – 127) × (1.110101(2)) = (-1)^1 × 2^(213 – 127) × (1.828125(10)) = - (2^86 × 1.828125)
(4) S = 0, E = 255, M = 011(2) E = 255이고 M ≠ 0이므로 NAN
(5) S = 0, E = 0, M = 011(2)
(-1)^0 × 2^(-126) × (0.011(2)) = (-1)^0 × 2^(-126) × (0.375(10)) = 2^(-126) × 0.375
3.22 부동소수점 표현은 가수(M) 필드의 최상위 비트에 항상 1이 저장되기 때문이다.
IEEE 754 표준 32-비트 부동소수점 형식에서의 E = 0, M = 0일 때, 0이 되므로
0 01111111 00000000000000000000000이다.
3.23
(1) 253.25(10) = 11111101.01(2) = 1.111110101(2) × 27
0 10000000110 1111101010000000000000000000000000000000000000000000
(2) -1.625(10) = -1.101(2) = (-1) × 1.101(2)
1 01111111111 1010000000000000000000000000000000000000000000000000
3.24
(1) (0.111001 × 2^(-5)) + (0.100111 × 2^(-3)) = (0.00111001 × 2^(-3)) + (0.100111 × 2^(-3)) = 0.110101 × 2^(-3)
(2) (0.100011 × 2^6) – (0.111001 × 2^3) = (0.100011 × 2^6) – (0.000111 × 2^6) = 0.111 × 2^6
(3) (0.1001 × 2^8) × (0.1011 × 2^12) = (0.01100011 × 2^(8 + 12)) = 0.01100011 × 2^20 = 0.1100011 × 2^19(정규화 표현) = 0.110010 × 2^19
3.25
(1) 1.42로 절삭한 경우 r = (1.427 – 1.42) / 1.427 = 0.007 / 1.427 ≒ 0.0049
1.43으로 반올림한 경우 r = (1.427 – 1.43) / 1.427 = (-0.003) / 1.427 ≒ -0.0021
(2) 문제 3.23이 아니라 문제 3.24입니다. (개정 4판에서 5판으로 수정하다 보니 생긴 오타 같습니다.)
3.24 – (1) : r = {(0.11010101 × 2^(-3)) – (0.110101 × 2^(-3)) / (0.11010101 × 2^(-3))} = 0.00000001 / 0.11010101 ≒ 0.0047
3.24 – (2) : r = {(0.111 × 2^6) – (0.111 × 2^6)} / (0.111 × 2^6) = 0(오차 없음)
3.24 – (3) : r = {(0.1100011 × 2^19) – (0.110010 × 2^19) / (0.1100011 × 2^19)} = (-0.0000001) / 0.1100011 ≒ 0.0101(1) 8-비트 길이의 부호화-크기 : 0001 0011
'📖 이론 > 컴퓨터구조론' 카테고리의 다른 글
| 컴퓨터 구조론 5판 6장 연습 문제 정답 (0) | 2023.06.06 |
|---|---|
| 컴퓨터 구조론 5판 5장 연습 문제 정답 (0) | 2023.06.06 |
| 컴퓨터 구조론 5판 4장 연습 문제 정답 (1) | 2023.06.06 |
| 컴퓨터 구조론 5판 2장 연습 문제 정답 (5) | 2023.06.06 |
| 컴퓨터 구조론 5판 1장 연습 문제 정답 (0) | 2023.03.14 |

